Магічні функціональні трикутники.

Оператор Вінницького на магічних трикутниках.

Реалізація гіпотези у вигляді генератора магічних трикутників

Аналогічні існують генератори для магічних квадратів

МАГІЧНІ ПРЯМОКУТНИКИ

МАГІЧНІ ПРЯМОКУТНИКИ

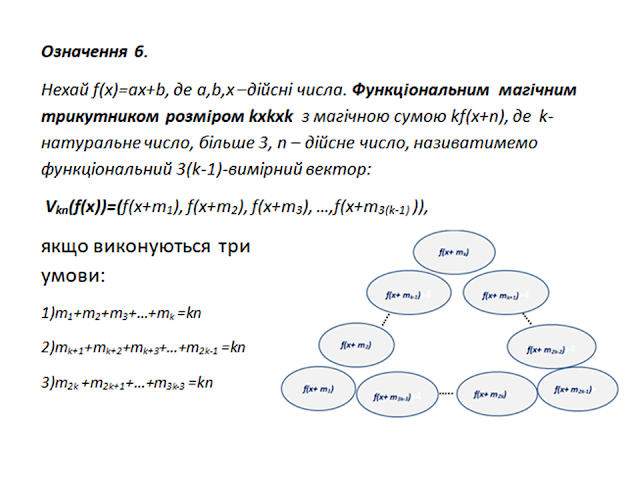
Означення. Клітинковий прямокутник, розміром nxm, називається класичним магічним прямокутником, якщо його клітинки заповнені натуральними числами від 1 до nxm так, що сума усіх чисел в кожному із стовпців однакова, сума усіх чисел в кожному з рядків однакова.

Приклад. Утворимо класичний магічний прямокутник, розміром 2x4, заповнений числами від 1 до 8.

Побудова.  Так сума усіх чисел в кожному із стовпців однакова і рівна 9, сума усіх чисел в кожному з рядків однакова 18. Адже, сума всіх чисел від 1 до 8 складає 8×9:2=36. Тому  в кожному із двох рядків сума мусить бути рівна 36:2=18, а в кожному із чотирьох стовбців ‒ 36:4= 9. 

Так, як для числової послідовності 1, 2, 3, …, 7, 8( вона є арифметичною прогресією і володіє цікавими властивостями)  виконується властивість «суми крайніх»:  1+8=2+7=3+6=4+5=9, то усі стовпчики можна заповнити парами чисел: (1; 8), (7; 2), (6; 3), (4; 5).

Так, як для числової послідовності 1, 2, 3, …, 7, 8 виконується властивість:  1+4 =2+3 =5; 5+8 = 6+7 =13; то маємо заповнення першого рядка четвірками чисел: (1; 4; 6; 7),  і другого рядка: (3; 8; 2; 5),  бо їх суми: 1 + 4 + 6 + 7 = 3 + 8 + 2 + 5 = 18.

1	4	6	7
8	5	3	2

Запитання: Чи вірно, що різних класичних магічних прямокутників розміром 2х4 не менше 24?

Відповідь: Усіх пар для заповнення стовпчиків рівно чотири: (1; 8), (7; 2), (6; 3), (4; 5). Використаємо комбінаторне «правило добутку». Перший стовпчик можна заповнити чотирма способами, тоді для другого стовпчика залишається тільки три пари, після того як заповнені перші два стовпчика, для третього стовпчика залишається тільки дві пари чисел, а вже для останнього стовпчика ‒ одна пара. Всього маємо 4×3×2×1 = 24 способів. Тепер, коли усі стовпчики заповнені, ми можемо, поміняти місцями рядки, і прямокутник залишиться магічним. Отже, 2×24 = 48 магічних прямокутників розміром 2х4 .

Приклад. В клітинковий прямокутник, розміром 3x5, заповнений числами від 1 до 15,

	1
				11

 зображений на малюнку впишіть числа від 2 до 15 за виключенням 11, яке вже вписано, так, щоб виконувались такі умови: сума трьох чисел в кожному із стовпців однакова; сума п'яти чисел в кожному з рядків однакова; сума кожних двох чисел верхньої та нижньої стрічки, які розміщенні симетрично центральної клітинки середньої стрічки також однакова.

Побудова. Сума всіх чисел від 1 до 15 складає 120. Отже, в кожному рядку сума мусить бути 40, а в кожному стовбці ‒ 24.  Суми чисел у всіх п’яти парах клітинок верхнього  та нижнього рядка становлять 80, отже, сума чисел в кожній парі 16. Ця сама сума повинна утворюватись в клітинках, симетричних відносно центру прямокутника. Отже, прямокутник заповнюється таким чином:

5
	1	8	15
				11

У другому стовбчику може бути або 14 і 9, або 13 і 10. Послідовним перебором переконуємося, що єдиний можливий варіант

5	14		7
	1	8	15
	9		2	11

Тепер заповнення будь-якої клітини визначає всі інші. Простою перевіркою знаходимо єдиний варіант

5	14	4	7	10
13	1	8	15	3
6	9	12	2	11

Запитання. Чи існують класичні магічні прямокутники довільних розмірів?

Відповідь: Не для всіх розмірів клітинкових прямокутників існують класичні магічні квадрати. Наприклад, класичний магічний прямокутник, розміром 2x3, заповнений числами від 1 до 6 не існує, бо сума чисел 1+2+3+4+5+6=21, непарне число, а прямокутник має парну кількість рядків.  По рядкам не можна утворити однакову суму чисел, проте по стовбцям, така сума рівна 21:3 = 7.  

Трикутні та квадратні числа та їх властивості

Трикутні та квадратні числа та їх властивості

Багатокутні числа

Натуральний ряд чисел починається з 1, а всі інші числа отримуємо додаванням до попереднього числа по одиниці. Природно прийти до думки скласти таку числову послідовність, яка починається з одиниці і утворює наступні числа додаванням до попереднього числа по 2, по 3, по 4 і так далі…

Таким чином утворюються послідовності чисел:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ……  n …..

1, 3, 5,  7,  9,  11, 13, 15, 17, …. 2n-1….

1, 4,  7, 10,  13, 16, 19, 21, ….. 3n-1….

1, 5, 9, 13, 17, 21, 25, 29, …..4n-1….

і так далі.

Знайдемо суми одного , двох, трьох, чотирьох  і так далі…

Утворяться такі послідовності:

1, 3, 6, 10, 15, 21, 28, …..  трикутні числа.

1, 4, 9, 16 , 25, 36, 49,…..  квадратні числа.

1, 5, 12, 22, 35, 51, 70, …. п’ятикутні числа.

1,  6, 15, 28, 45, 66, 91, … шестикутні числа 

і так далі

Ці числа зустрічаються у піфагорійців (VI в. до н. е.) і потім у подальших грецьких математиків (Ератосфен, Гипсикл). Особливо детально вивчали їх математиків перших століть 158 нашої ери: Нікомах, Теон Смірнській (II в.) і їх сучасники. Цим захоплювався і батько грецької алгебри Діофант III-IV ст. н. е.), що написав про них цілу книгу, що дійшла до нас.

Незалежно від грецьких математиків багатокутними числами займалися індійські і китайські математики.

Грецьких математиків знайшли різні властивості багатокутних чисел, які в більшості випадків доводилися на фігурах.

Теорема. Довести, що довільне восьмикутне число рівне сумі шести (n - 1)-х трикутних чисел плюс n.

Правильність теореми видно з таблиці: друге восьмикутне число 8 = 6∙1 + 2; третє: 21 =6∙3 + 3, четверте: 40 = 6 ∙ 6 + 4,  п'яте:  65 = 6∙10 + 5 і так далі.

Для доказу досить побудувати креслення і сказати, за зразком індійського керівництва: дивися!

Дуже важкі теореми про багатокутні числа доводили П’єр Ферма (XVII в.), Леонард Ейлер і Лагранж (XVIII в.), Карл Гаус (XIX в.) і ін. Ці теореми грали і грають велику роль у вищій арифметиці.

Найважливішою з цих теорем є теорема, яку Ферма назвав «золота»: всяке натуральне число є або трикутне або сума двох або трьох трикутних чисел; або квадратне або сума двох, трьох або чотирьох квадратних чисел; або п'ятикутне або сума двох, трьох, чотирьох  або п'яти п'ятикутних чисел і так далі. Ферма не міг дати доведення цієї теореми, що слідує, за його словами, «з багатьох глибоко прихованих таємниць чисел». Пройшовши через руки Ейлера, Лагранжа, Лежандра і Гауса, теорема Ферма була повністю доведена французьким математиком Коші (1813-1915 рр.). З цієї теореми витікають багато важливих    властивостей пропозиції теорії чисел.

Зазначимо, що в європейській математиці зустрічаються ще фігурні числа, цими числами у європейських математиків називалися коефіцієнти членів ступенів бінома (а+b)ⁿ  при n = 1, 2, 3, 4... , тобто числа з трикутника Паскаля.

Трикутні  числа

Як відомо,   трикутними   називаються   числа,   утворені  шляхом   послідовного  підсумовування  чисел натурального   ряду,   тобто   числа 

1=1                                                     1    3   6    10     15    21

1+2 =3                                                   2   5    9     14     20

1+2+3= 6                                                 4   8    13     19     

………………                                           7    12   18

1+2+3 + …… + n = 0,5n(n+1)                   11    17

…………………………………           16

Трикутне число рівне половині добутку двох сусідніх чисел натурального ряду, тобто Т_n = 0,5n(n+1).

Позначають трикутні числа таким чином:

Т₁ = 1,  Т₂ = 3,  Т₃ = 6, Т₄ = 10, Т₅ = 15, Т₆ = 21, Т₇ = 28, Т₈ = 36, Т₉=  45, Т₁₀ =  55, Т₁₁ = 66, Т₁₂ = 78, Т₁₃= 91, Т₁₄ = 105, … , Т_n = 0,5n(n+1), …

Трикутні числа володіють безліччю цікавих властивостей.

Так, сума двох послідовних трикутних чисел рівна квадратному числу

Т_n-1   +  Т_n = 0,5n(n-1) + 0,5n(n+1)  = 0,5n² + 0,5n² + 0,5n - 0,5n =  n².               (1)

Або   

Т_n =  n²  – Т_n-1.

а їх різниця

Т_n+1   –  Т_n = 0,5n(n-1) - 0,5n(n+1)  = 0,5n² – 0,5n² + 0,5n - 0,5n =  n.                      (2)

Або  

Т_n =  Т_{n -1}  +  n  .

Квадратні числа

Квадратні числа  числами вважають результат множення натурального числа на самого себе, іноді цю дію означають, як  другу степінь (квадрат) натурального числа. Приклади таких чисел:

К₁ = 1,  К₂ = 4,  К₃ = 9, К₄ = 16, К₅ = 25, К₆ = 36, К₇ = 49, К₈ = 64, К₉=  81, К₁₀ =  100,

К₁₁= 121,  К₁₂ =144, К₁₃= 169, К₁₄ =196, … , К_n = n∙n = n², …

 1       4      9     16    25

 2       3      8     15    24

 5       6      7     14    23

10     11    12    13    22

17      18    19   20    21

Зв'язок між трикутними та квадратними  числами

Трикутні і квадратні числа зв'язані між собою багатьма співвідношеннями. Вкажемо тільки наступні, знайдені нами залежності:

3×Т_n – Т_n-1   + 1= (n + 1)²  = К_n+1                                  (3)

2×Т_n×Т_2n  /  Т_2n-1    = n²  = К_n                                   (4)

Т_2n(n+1)  /  Т_n    = (2n + 1)² = К_2n+1                              (5)

Із формули (5), наприклад, при n = 5 маємо:

(  Т₆₀   / Т₅  )- 1 = 11².

Широко відома так звана формула Діофанта

8×Т_n  + 1 = (2n + 1)²,

або     

Т_n = 0,125((2n + 1)² -  1) = 0,125К_2n+1 – 0,125   (6)

Здавалося б, трикутні числа та квадрати взаємозв'язані вельми просто. Але знаменитий математик Л. Ейлер (1707- 1783) поставив таке завдання: знайти формулу для трикутних чисел, що одночасно є квадратами. Що такі числа є, легко переконатися. Так, вже Т₁ = 1 = 1², Т₈ = 36 = 6².

А далі?  Ейлер   дав    формулу   для    отримання   квадратних   чисел (піднесену нами в квадрат):

К_n  = ((3 + 2^1,5)ⁿ –  (3 –2^1,5)ⁿ )² × 2^-2,5                    (7)

При n =1 і n = 2 з неї отримуємо вже відомі нам числа 1 і 36, при n = 3 маємо К₃  = 3², при n = 4,  К₄  = = 204² і т.д.

Формула (7) здалася Ейлерові дуже складною, і він запропонував іншим ученим спростити її або знайти іншу, простішу, але висловив при цьому припущення, що це, очевидно, найпростіша зі всіх можливих формул. Мабуть, це так і є, тому що до цих пір ніхто не запропонував більш простій залежності.

Про представлення  трикутних     чисел    квадратами

А що можна сказати про суму трьох  і чотирьох послідовних трикутних чисел?

Чи може така сума бути квадратом? Це завдання, не дивлячись на її простоту, до цих пір не ставилося. Тим часом такі трійки і четвірки трикутних чисел існують. Так, маємо трійки послідовних трикутних чисел:

Т₅ + Т₆ + Т₇ = 8².

Т₁₄ + Т₁₅+ Т₁₆ = К₁₉ = 19²,

або

105 + 120 + 136 = 361 = 19²

Т₆₃ + Т₆₄ + Т₆₅ = К₇₉ = 79²

Т₁₅₂ + Т₁₅₃ + Т₁₅₄ = К₁₈₈ = 188² .

Можна відзначити, що квадратні числа, що є одночасно сумою трьох послідовних трикутних чисел, повинні бути також виду 3Т_n + 1.

Тому

Т_n-1   + Т_n  +  Т_n+1   = 3Т_n + 1.

Існують і четвірки послідовних трикутних чисел, в сумі ті, що дають квадратне число. Наприклад:

Т₅ + Т₆ + Т₇  + Т₈ = К₁₀  = 10²

Т₃₉ + Т₄₀ + Т₄₁ + Т₄₂ = К₅₈ = 58²

Т₂₃₇ + Т₂₃₈ + Т₂₃₉  + Т₂₄₀ = К₃₃₈  = 338²

Т₁₃₉₁ + Т₁₃₉₂ + Т₁₃₉₃  + Т₁₃₉₄ = К₃₃₈  = 1970²

Ці формули, втім, як і попередні, можуть бути узагальнені, наприклад, таким чином:

Т_3к-1 + Т_3к + Т_{4к -1} + Т_4к = (5к)² = (3к)² +(4к)² .         (8)

При к =1 звідси маємо

Т₂ + 2Т₃ + Т₄ = 5² або 3 + 6 + 6 + 10 = 25 = 5²,

при к=2 отримаємо приведену раніше формулу,  при к = 7 маємо

Т₂₀ + Т₂₁ + Т₂₇ + Т₂₈ = 35²

і т.д.

Звернемо увагу на праву частину формули (8). Вона відображає факт, що вже наголошувався (див. формулу (1)): сума двох послідовних трикутних чисел рівна квадратному числу. Але таким чином знаходження загальної формули для четвірок трикутних чисел виявляється безпосередньо взаємозв'язано з піфагоровимі числами! А саме: якщо піфагорійці знайшли тотожність, що охоплює трійки чисел, в яких числові значення катета і гіпотенузи є сусідніми числами в натуральному ряду:

(2n + 1)² + (2n²  + 2n)² = (2n² + 2n + 1)²                   (9)

де n = 1,2,3,4      то нам треба знайти піфагорові трійки, у яких послідовними числами є величини катетів, т. е необхідно знайти числа, що задовольняють рівнянню а² + (а + 1)² = с².

Такі трійки піфагорових чисел є. Ось вони:

3² + 4²=5²,

20² + 21²=29²,

119²+120²=169²

і т.д.

    Формула для знаходження квадратних чисел, що є      сумою  двох   послідовних   квадратних чисел, має наступний вигляд:

С_n = 2 ^-1,5×((1+ 2^0,5)^2n-1 – (1- 2^0,5)^2n-1)                                                (10)

Числова послідовність, що виходить звідси при n  = 1,2,3         така:

1, 5, 29, 169, 985, 5741 ... .   (11)

А формула для знахождення всіх четвірок послідовних трикутних чисел, в сумі тих, що дають квадратне число, така:

К_n = ( 2 ^-0,5×((1+ 2^0,5)^2n-1 – (1- 2^0,5)^2n-1))²                              (12)

Числова послідовність сум таких четвірок має вигляд:

2², 10²,  58², 338², 1970²,11482²  ….                   (13)

Відзначимо ще, що для всіх трьох послідовностей, що розглядаються тут, описуються формулами (7), (10) і (12), справедливе одне і те ж рекурентне співвідношення

а_n+1 = 6а_n – а_n-1,

причому для послідовності 1, 6, 35, 204, 1189..., загальний член якої описується формулою Ейлера (7)

а_о = a₁ =1,

для послідовності (11)

а_о= a₁ =1

 і  для послідовності (13) (але без піднесення кожного члена в квадрат)

а_о = a₁ =2.

Трійки трикутних чисел,

Т₅ + Т₆ + Т₇ = 8².

Т₁₄ + Т₁₅+ Т₁₆ = К₁₉ = 19²,

Т₆₃ + Т₆₄ + Т₆₅ = К₇₉ = 79²

Т₁₅₂ + Т₁₅₃ + Т₁₅₄ = К₁₈₈ = 188²,

є членами числової зворотної послідовності

 1, 2, 8, 19, 79, 188, 782...

Будь-який член цієї послідовності, що стоїть на непарних місцях, можна знайти по формулі

К_n = 4^-1×6^-0,5(39 + 16×6^0,5)(5 + 2×6^0,5)ⁿ – (39 – 16×6^0,5)(5 – 2×6^0,5)ⁿ )                    (14)

де n = 0, 1, 2, 3...

Будь-який член послідовності, що стоїть в ній на парних місцях, знаходиться по формулі

К_n = 4^-1×6^-0,5(9 + 4×6^0,5)(5 + 2×6^0,5)ⁿ – (9 – 14×6^0,5)(5 – 2×6^0,5)ⁿ )                   (15)

де n = 0, 1, 2, 3...

        

Формулі (14) відповідає рекурентне співвідношення

а_2n+3 = 10а_2n+1 –  a_2n-1.

a₁ = 1,  a₃  = 8, а₅ = 79, а₇  = 782;   а₉ =  7741

Для чисел, що стоять на парних місцях послідовності, рекурентне співвідношення має вигляд:

а_2n+4 = 10а_{2n + 2}  – а_2n,

а₂ = 2, a₄ = 19, а₆ =188,…

Отже, знайдені формули для обчислення піфагорових чисел, що є послідовними квадратами, яким рівні катети прямокутного трикутника, а також трійки і четвірки послідовних трикутних чисел, що в сумі мають квадратне число. Видно, груп по 5 і по 6 послідовних трикутних чисел квадратами бути не можуть. Але це питання поки залишається відкритим.

Повертаючись до формули Діофанта (6), відзначимо, що нам вдалося її узагальнити таким чином:

(kn + 1)² = 8(k-1)Т_n+((k-2)n – 1) ².  (16)

Дана формула дозволяє представити будь-яке квадратне число у вигляді суми меншого квадрата і кратного трикутному числу числа.

З (16) якщо k = 1 маємо тривіальну тотожність

(n+1) ² =  (- n - 1)² ,

 при k =2 отримуємо залежність Діофанта (6),

при k =3 маємо

(3nа + 1)² = 16T_n + (n - 1)²,

при к = 4

(4nа + 1)² = 24T_n + (2n - 1)²

і т. д.

Відповідно до формули (16) квадратні числа можуть мати різне число представлень у вигляді вищезгаданої суми. Причому якщо kn - просте, то число представлень рівне лише двом. Якщо ж kn складене число, то число уявлень залежить від числа дільників kn. Наприклад, якщо kn = 35, то маємо наступні розкладання:

(1×35+1)²=8.0.Т₃₅+36²,

(5×7+1)²=8.4Т₇+20²,

(7×5+1)²=8×6 Т₅+24²,

(35×1 + 1)²=8×34Т₁+32².

Як   бачимо,   при   розкладаннях   враховується   і   одиниця.

Для простих kn це видно особливо наочно. Так, для

kn = 5 маємо:

(5+1)² = 6²  = (1×5+1)² = 8×0×Т₈+ 6²  = (5×1 + 1)² = 8×4Т₁ +  2².

На закінчення вкажемо на наступне. Якщо розглядати не тільки квадратні, а будь-які натуральні числа у вигляді уявлення їх сумою трикутних чисел і при цьому не вимагати, щоб трикутні числа були послідовними, то приходимо до знаменитої проблеми теорії чисел, якою займалися Ферма, Ейлер, Лагранж та інші. Ці математики виявили і показали, що будь-яке число можна представити у вигляді суми n-кутних чисел, що складається не більше ніж n доданків. Зрозуміло, що для представлення квадратного числа достатньо суми трьох трикутних чисел.