Магічний квадрат 4х4

Магічний квадрат 4х4

Утворення магічного квадрата 4х4.

Цей магічний квадрат 4х4, знайдений в Індії  – це найраніший унікальний магічний квадрат виявлений в написі XI століття в індійському місті Кхаджурахо:

7	12	1	14
2	13	8	11
16	3	10	5
9	6	15	4

Це перший магічний квадрат, що відноситься до різновиду так званих "диявольських" квадратів.

Квадрат Альбрехта Дюрера

Фрагмент гравюри Дюрера

Магічний квадрат 4х4, зображений на гравюре Альбрехта Дюрера «Меланхолія I», вважається найранішим в європейському мистецтві. Два середні числа в нижньому ряду указують дату створення картини (1514).

Отже, якщо перші 16 натуральних чисел розмістити в клітинках квадрата 4х4 так, щоб виконувалась така умови: сума  по усіх рядках, по усіх колонках, по двох діагоналях була однакова, то отримаємо нормальний магічний квадрат 4х4 з магічною константою 34.

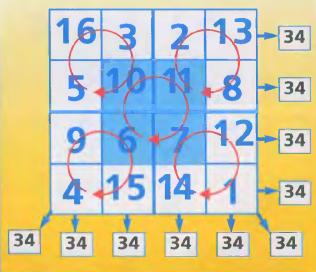
Переходимо до методу побудови магічного квадрату 4х4, який називається “Метод Рауз-Болла”. Він полягає в наступному: у даний квадрат 4х4 вписуються числа в їх природному порядку, починаючи з лівого верхнього кута. Потім в квадраті проводяться діагоналі. Числа, розташовані у взаємно симетричних клітках (щодо центру квадрата), через які пройшли діагоналі, міняються місцями, а числа, через які діагоналі не пройшли, залишаються на місці. Так, на малюнку діагоналі перетнули вісім чисел, треба поміняти місцями взаємно симетричні: 1-16, 6-11, 13-4, 10-7. Готовий магічний квадрат зображений на малюнку.

16	3	2	13
5	10	11	8
9	6	7	12
4	15	14	1

Тепер досліджуємо магічний квадрат 4х4 для натуральних чисел від 1 до 16 чисел. Сума цифр по горизонталях, вертикалях, діагоналях 0,5(4×4+1)×4 = 34, крім того сума кожного із 4 окремих квадратів із 4 кутових клітин рівна 34, сума центрального квадрата із 4 клітин рівна  34, сума усіх 4 кутів рівна 34, сума усіх крайніх чисел через 2 клітини рівна 34, Сума двох крайніх протилежних клітин рівна 34 (2+3+14+15) або (8+12+5+9).  Сума двох протилежних чисел крайніх до різних кутів рівна 34 (2+13+4+15) або (14+1+16+3) = 34; (12+1+16+5) = 34; (13+8+9+4) = 34, сума 4 клітин, що лежать з обох сторін протилежних кутів також дорівнює 34 = (5+3+12+14) або (2+8+9+15).

Утворення магічного квадрату 4х4 з 16 членів арифметичної прогресії

 Якщо дана арифметична прогресія з 16 членів:

а,  а + d,  а + 2d,  а +3d,  а + 4d, а +5d,  а + 6d,  а +7d,   а+8d, …, а + 14d, а + 15d

Тоді можна з цих чисел утворити магічний квадрат 4х4 з магічною константою 4а +30d:

а + 15d	а + 2d	а + d	а + 12d
а + 4d	а + 9d	а + 10d	а + 7d
а + 8d	а + 5d	а + 6d	а + 11d
а + 3d	а + 14d	а + 13d	а

Наводимо приклади магічних квадратів із 16 клітин. Розглянемо можливі варіанти розміщень в 16–клітинному магічному квадраті різних послідовностей рядів чисел.

    0, 1, 2, 3, 4, 5, 6, 7 , 8, 9         1, 2, 3, 4, 5, 6, 7, 8, 9, 10         1,3, 5, 7, 9, 11, 13, 15, 17 

       10, 11, 12, 13, 14,15             11, 12, 13, 14, 15, 16               19, 21, 23, 25, 27, 29, 31    

                                                                      

15	2	1	12		16	3	2	13		31	5	3	25
4	9	10	7		5	10	11	8		9	19	21	15
8	5	6	11		9	6	7	12		17	11	13	23
3	14	13	0		4	15	14	1		7	29	27	1

      Вертикаль                            Вертикаль                          Вертикаль                                                       

      Діагональ    =30                   Діагональ  =34                    Діагональ =64

      Горизонталь                        Горизонталь                       Горизонталь     

0,  2, 4, 6, 8, 10, 12, 14, 16,                    2, 4, 6, 8, 10, 12, 14, 16, 18,

18, 20, 22, 24, 26, 28, 30,                     20, 22, 24, 26, 28, 30, 32

30	4	2	24		32	6	4	26
8	18	20	14		10	20	22	16
16	10	12	22		18	12	14	24
6	28	26	0		8	30	28	2

   Вертикаль                                       Вертикаль                        

   Діагональ    =60                              Діагональ  =68                 

   Горизонталь                                   Горизонталь                     

     

Попередні  5 видів послідовного ряду чисел від 0 до 15, від 1 до 16, непарного ряду від 1 до 31 та парних послідовних рядів чисел від 0 до 30, та від 2 до 32  складені з послідовних ланцюжків  арифметичних прогресій.

Деякі властивості магічного квадрату  4х4

Варіантів розстановок чисел від 1 до 16 на  квадратній матриці 4х4 рівне 2 в шістдесят четвертому ступеню мінус 1. Це дуже велике число.

Кожне кореневе число від 1 до 16 (тобто число стоїть у верхньому лівому кутку матриці 4 х 4) дає 54 кореневих рядки, кожний з яких дає 4 магічних квадрата. Таким чином загальне число рядків рівне 864 (30 в квадраті мінус 6 в квадраті) а число магічних квадратів четвертого порядку рівне 3456. Краса полягає в тому, що це число виражається зокрема, як різниця квадратів 60 і 12 і в той же час як дубрток 2 в 7 ступені на 27.

16	3	2	13
5	10	11	8
9	6	7	12
4	15	14	1

Маємо 16 кореневих чисел, що утворюють 864 магічних рядків в квадраті 4х4. Це є різниця квадратів чисел 30 і 6! (30² – 6² = 900 – 36 = 864) Кожний з цих рядків породжує рівно 4 магічних квадрати.
Таким чином, відкривається закономірність: 3600 - 144 = 60² – 12² = 3456.

Усіх магічних квадратів 4х4 утворених з натуральних чисел від 1 до 16 рівно 3456.  І це не рахуючи їх віддзеркалень і поворотів.

 Сума чотирьох чисел центрального квадрату 2х2, що розташовані у центрі магічного    квадрата 4х4 рівна магічному числу 34.

 Сума чотирьох чисел квадрату 2х2, що містять дві діагональні клітинки магічного    квадрата 4х4 рівна магічному числу 34.

 Середнє арифметичне усіх чисел магічного квадрату 4х4 рівне чверті магічного числа 8,5.

А1	А2	А3	А4
В1	В2	В3	В4
С1	С2	С3	С4
D1	D2	D3	D4

Cума рівна 34-м не тільки по вертикалях, горизонталях і діагоналях, а і в клітинках:

a1, a4, d1, d4;

a2, a4, c2,  c4;

a3, a4, b3,  b4;

с1, в1,  в4,  с4;

а2, а3,   d2,  d3.

Спосіб утворення магічних квадратів 4m х 4m

Магічним квадратом парно-парного порядку називається квадрат порядку 4m х 4m (m=1,2,3…), тобто порядок такого квадрата ділиться на 4. Простий квадрат парно-парного порядку - це квадрат четвертого порядку. Відомо принаймні два методи побудови магічних квадратів парно-парного порядку. Перший називається методом квадратних рамок. Розглянемо його на прикладі магічного квадрата восьмого порядку. На матричне поле (із зображеним на нім початковим квадратом 8х8) наносяться квадратні рамки 4х4, із стороною в два рази меншого розміру, ніж сторона початкового квадрата

			4	5
		3			6
	2		21	20		7
1		22			19		8
16	23		36	37		18	9
24	15	35			38	10	17
25	34	14	53	52	11	39	32
33	26	54	13	12	51	31	40
48	55	27			30	50	41
56	47		28	29		42	49
57		46			43		64
	58		45	44		63
		59			62
			60	61

з кроком в одну клітку по діагоналі (або дві клітки по рядках і стовпцях). Потім по лініях рамок розставляються числа від 1 до n2 по порядку, починаючи з лівого верхнього кута початкового квадрата, причому перша рамка обходиться за годинниковою стрілкою, друга рамка починається з верхньої вільної справа клітки

1	58	22	45	44	19	63	8
16	23	59	36	37	62	18	9
24	15	35	60	61	38	10	17
25	34	14	53	52	11	39	32
33	26	54	13	12	51	31	40
48	55	27	4	5	30	50	41
56	47	3	28	29	6	42	49
57	2	46	21	20	43	7	64

квадрата і обходиться проти годинникової стрілки і т.д. Числа, що не потрапили в квадрат, переносяться всередину його так, щоб вони прилучилися до протилежних сторін квадрата. Готовий магічний квадрат зображений на малюнку.

1	2	3	4		16	2	3	13		1	15	14	4
5	6	7	8		5	11	10	8		12	6	7	9
9	10	11	12		9	7	6	12		8	10	11	5
13	14	15	16		4	14	15	1		13	3	2	16

Пропоную побудувати цим методом магічний квадрат дванадцятого порядку.

Переходимо до другого методу побудови парно-парних магічних квадратів, який називається “Метод Рауз-Болла”. Він полягає в наступному: у даний квадрат парно-парного порядку вписуються числа в їх природному порядку, починаючи з лівого верхнього кута. Потім в квадраті проводяться діагоналі. Числа, розташовані у взаємно симетричних клітках (щодо центру квадрата), через які пройшли діагоналі, міняються місцями, а числа, через які діагоналі не пройшли, залишаються на місці. Так, на мал. 8 діагоналі перетнули вісім чисел, треба поміняти місцями взаємно симетричні: 1-16, 6-11, 13-4, 10-7. Готовий магічний квадрат зображений на малюнку. Можна поступити навпаки: залишити на місці числа, через які пройшли діагоналі, а поміняти місцями числа, що не потрапили на діагоналі і симетрично розташовані щодо центру квадрата. На мал. 10 показаний квадрат, побудований таким чином. Порівнявши його з квадратом на мал. 9, ви бачите, що це той же квадрат, повернений на 180 градусів щодо центру квадрата.

При побудові методом Рауз-Болла магічного квадрата восьмого порядку діагоналі сполучають не тільки кути квадрата, але і середини його сторін, тобто діагоналі проводяться в чотирьох  кутових квадратах 4х4 (див. малюнок); взаємно симетричних пар чисел, які треба поміняти місцями, буде шістнадцять: 1-64, 10-55, 19-46, 28-37, 8-57, 15-50, 22-43, 29-36, 4-61, 5-60, 11-54, 14-51, 18-47, 23-42, 25-40, 32-33. На малюнку зображений готовий магічний квадрат восьмого порядку, побудований методом Рауз-Болла.

1	2	3	4	5	6	7	8		64	2	3	61	60	6	7	57
9	10	11	12	13	14	15	16		9	55	54	12	13	51	50	16
17	18	19	20	21	22	23	24		17	47	46	20	21	43	42	24
25	26	27	28	29	30	31	32		40	26	27	37	36	30	31	33
33	34	35	36	37	38	39	40		32	34	35	29	28	38	39	25
41	42	43	44	45	46	47	48		41	23	22	44	45	19	18	48
49	50	51	52	53	54	55	56		49	15	14	52	53	11	10	56
57	58	59	60	61	62	63	64		8	58	59	5	4	62	63	1

Застосування  магічних квадратів на практиці

Магічні квадрати 4х4 широко застосовувались для виписування зашифрованого тексту за наведеною у таблицях нумерацією. Якщо потім виписати склад таблиці по рядкам, то отримаємо шифровку перестановкю букв. Вважалось, що створені за допомогою магічних квадратів кодування оберігає не тільки ключ, але і магічна сила. Ось приклад магічного квадрату і кодування:
16 3 2 13                   О И Р Т
5 10 11 8                   З Ш Е Ю
9 6 7 12                     Ж А С 
4 15 14 1                   Е Г О П
 Отримана із словосполучення утвореного російською мовою «ПРИЕЗЖАЮ ШЕСТОГО», закодована так «ОИРТЗШЕЮ ЖАСЕГОП» таки  є досить складною.
Все нове, це добре забуте старе.
 Микола Михайлович Рудін поклав своє життя на те, щоб довести, що шахи відбулися з ворожінь на магічних квадратах. Відома стародавня легенда про мудреця, який попросив покласти на кожну клітку дошки в два рази більше зерен, ніж в попередню... Важливість цієї легенди для нас полягає в тому. що число зерен витребуваних мудрецем в точності дорівнює числу ... розстановок чисел від 1 до 16 у матриці 4х4. Гра так і називалася: ЧАТУРАНГА (від слова "чотири") У всіх чотирьох кутках дошки ставилися 4 війська по 4 фігури в кожному...  Для НЕОБІЗНАНИХ в магії у стародавні часи давалося неповне визначення магічного квадрата, для присвячених (Піфагорійський союз і інші закриті школи) – існувало повне означення. 216 красивих квадратів в кожному з яких зашито всі 54 рядки (четверта Чакра Анахата має, між іншим, 54 промені!) магічних квадратів, що породжують серію. Питання про "магічне" число 34 - особливе питання.

Згідно повідомленню Бурдіна (у книзі "Гри у сімейному колі" Перм, 1991) всього відомо 880 магічних квадратів четвертого порядку, тобто на матриці 4х4. Не рахуючи їх віддзеркалень і поворотів. Є повідомлення про доведеність існування 11 незалежних магічних квадратах четвертого порядку, що не зводяться один до одного. Якщо побудувати Майстра магічних квадратів, тобто програму, яка дозволяє проаналізувати ВСІ вірогідні розстановки і переконатися, що кожне кореневе число від 1 до 16 (тобто число стоїть у верхньому лівому кутку матриці 4 х 4) дає 54 кореневих рядки, кожний з яких дає 4 магічних квадрата. Таким чином загальне число рядків рівне 864 (30 в квадраті мінус 6 в квадраті) а число магічних квадратів четвертого порядку рівне 3456. Краса полягає в тому, що це число виражається зокрема, як різниця квадратів 60 і 12 і в той же час як дубрток 2 в 7 ступені на 27 (числа, що оздоблюють числовий ряд).

Магічний квадрат   n x n

Сума будь-якого стовпчика/рядка /діагоналі  магічного квадрату   n x n

фіксована, і рівна

М = n(n²+1)/2 = 0,5n(n²+1).

Доведення: Нехай  маємо магічний квадрат nхn з магічною константою   М( це сума будь-якого стовпчика/рядка /діагоналі МК  і сумою усіх чисел S. Тоді  сума  усіх чисел цього квадрату за формулою арифметичний прогресії рівна

1 + 2+ 3 + 4 + 5 +  …. + n² – 1 + n² = 0,5n²(n²+1)

Всього у магічному квадраті  nхn  рівно n  рядків.

Тому в кожному рядку сума чисел рівна

M = S/n = 0,5n²(n²+1)/ n = n(n²+1)/2= 0,5n(n²+1).  .

    Середнє арифметичне усіх чисел магічного квадрату nхn рівне магічному числу поділеному на n.

Доведення:
Нехай  маємо магічний квадрат nхn з магічною константою   М  і сумою усіх чисел S. Тоді  сума в кожному рядку рівна M = S/n. Обидві частини рівності   помножимо на 1/ n, отримаємо M/n = S/n² , де S – сума усіх чисел магічного квадрату , n² – кількість чисел магічного квадрату, S/n²  – середнє арифметичне усіх чисел магічного квадрату nхn .

Проблема принципу утворення магічних квадратів

Враховуючи властивості магічних квадратів(МК) (сума будь-якого рядка рівна сумі будь-якого стовпця  рівна сумі головної  діагоналі), для n² невідомих можна побудувати 2n + 1 однорідне лінійне рівняння, (розділ лінійної алгебри), тобто, треба скласти однорідну систему лінійних алгебраїчних рівнянь(СЛАР) і розв’язати.
Ранг матриці цієї СЛАР рівний 2n. Це означає, що 2n елементів магічного квадрату визначається рівняннями, а інші елементи ( всього їх n²-2n  елементів) – вільні, тобто невизначені, таким чином, вони приймають будь-які незаборонені значення (натуральні числа від 1 до n²).
Таким чином, магічний квадрат розмірності nхn, виходячи тільки із СЛАР, визначаються (n-2) рядками. Але СЛАР не знає, що сума будь-якого стовпчика/рядка /діагоналі МК фіксована, і рівна S=0,5n(n²+1). Тому ще n-2 елементів виявляються лінійно залежними.
Звідси можна зробити нове уточнення кількості варіантів магічних квадратів розмірності nхn (число сполучень (n²-3n+2) елементів з n² можливих):

N₂= (n²)!/(3n-2)!
Далі можна розв’язати нерівності в сітці натуральних чисел...Але це вже питання серйознішого дослідження.
Для порівняння, декілька чисел:

n=2:     (2²)^(2 ²)=256      : (2²)!=24 :    N₂=1
n=3:                   (3²)^(3 ²)~10⁸   : (3²)!~=10⁵:            N2 = 72
n=4:                     (n^2)^(n^2)~10^19 :  (n^2)!~=10^13:             N2 = 5765760
n=5:                          (n^2)^(n^2)~10^34 :  (n^2)!~=10^25:         N2 ~= 10^13

Розв’язок на ЕОМ магічного квадрату розмірності 5х5 теж "не за горами,  якщо кожне рішення-кандидат утворювати і перевіряти за 100 циклів гіга-герцового комп'ютера (10^7 Мк/сек), то ми знайдемо всі рішення за 10^6 сік, тобто менш, ніж за два тижні роботи такого комп'ютера. Використовуючи  4 процесори (завдання легко параллелізуєтся), ми вирішимо її в 3 дні. Первинна оцінка (10^19) взагалі не давала шансів на це навіть у разі МК розмірності 4.
У програмі не потрібно складати числа, а тільки перевіряти їх відповідність діапазону і повторення елементів між собою (у СЛАР, яка дає нам розв’язок, немає таких умов).
Програма, заснована на описаних принципах, знайшла:
-  для 3х3:   маємо  8 магічних квадратів з 72 (72=8*9)
- для 4х4:   маємо  7040 магічних квадратів  з 5765760  (5765760=7040*819)

Є і інші способи зменшити кількість вільних змінних, тому оцінка N2 не претендує на закінченість. У ідеалі, повинна бути якась проста формула типа

Nмк(n)=(n^2)!/(3n-2)! / F(n).

Гіпотеза про кількість магічних квадратів

Варіантів розстановок чисел від 1 до 16 на  квадратній матриці 4х4 рівне 2 в шістдесят четвертому ступеню мінус 1.
А ось число виникаючих магічних квадратів 4х4 за нашими уточненими даними рівне 3456! Таким чином, число магічних квадратів 4х4 не 880,  а 3456.

16 кореневих чисел утворюють 864 магічних рядків. Кожний з цих рядків породжує рівно 4 магічних квадрати.
Таким чином, відкривається якась закономірність: 3600 - 144 = 3456 = 60² – 12².
Але ЦЕ КВАДРАТИ ЧИСЕЛ 60 і 12!
Число рядків , що утворюють магічні квадрати  4х4 рівне 864.
Це також різниця квадратів чисел 30 і 6 ! (900 - 36)
Число магічних  квадратів 3х3 рівне 8, але і це різниця квадратів чисел 3 і 1!
Гіпотеза: ЧИСЛО МАГІЧНИХ КВАДРАТІВ БУДЬ-ЯКОГО ПОРЯДКУ Є РІЗНИЦЯ КВАДРАТІВ ЧИСЕЛ

Теорема ця вельми цікава і для магічних квадратів 3 і 4 порядки доведена.